1의 개수 세기

백준 9527

GOLD II

1. 문제 내용
2. 해결 방안
3. 풀이 코드

---

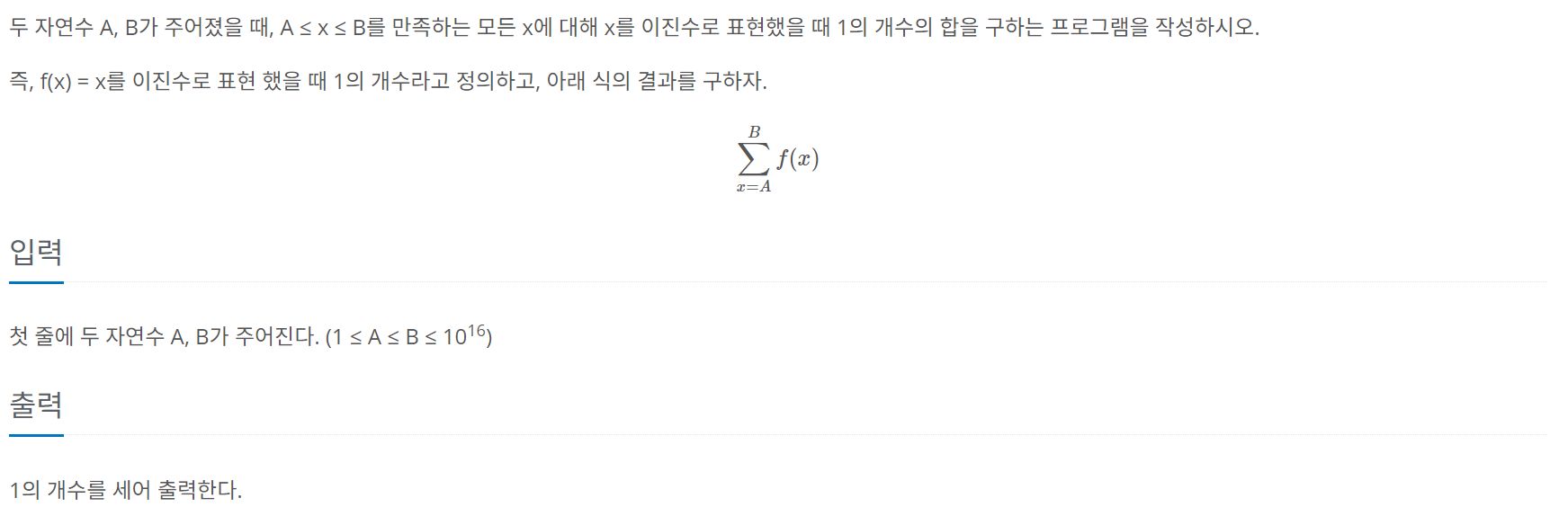
문제 내용

문제 링크

해결 방안

그림을 동반한 설명은 이 블로그를 참고하기 바란다. 문제에 따르면, 자연수 A, B에 대해 [A, B]의 범위에 있는 모든 자연수의 비트 중 1의 총 개수를 구하는 문제이다.

먼저, 각 2의 거듭제곱에 대해 [1, 2ⁿ-1]의 범위에 있는 비트 내 1의 개수를 각각 구한다. 그 다음, A와 B의 최상위 비트부터 훑으며 1의 개수를 누적하여 계산한다. 계산 방식은 현재 비트가 1인 경우, 현재 비트의 값 이전까지의 모든 1의 개수를 합하면 된다. 예로 들어, 현재 비트가 5번 비트인 1xxxx이라면, 0000~1111까지의 모든 1의 개수를 찾는다. 찾은 1에 개수에 추가적으로 현재 비트가 사용되는 횟수를 더해야 한다. 현재 비트가 사용되는 횟수는 현재 비트를 i번 비트라고 한다면, (현재 값 | (2^(i+1)-1)) - (2^i-1)와 같다. 만약 비트를 훑는 과정에서 1이었던 각 비트를 매번 지웠다면, 현재 비트가 사용되는 횟수는 현재 값에 2^i-1만 빼주면 된다.

해당 과정을 A와 B에 대해 모두 수행하면, 각각 A까지의 1의 개수와 B까지의 1의 개수가 나온다. A≤B라는 조건에 따라, B까지의 1의 개수에 A까지의 1의 개수를 빼주면 A와 B 사이의 1의 값이 나온다. 그러나, A가 범위에 포함되어 있으므로 위의 과정을 수행하기 전에 A에 1을 빼주어야 한다.

비트마스킹(Bit Masking)이란?

컴퓨터 과학에서 하나 이상의 인접 비트로 구성된 자료 구조를 비트 필드(bit field)라고 부른다. 흔히 말하는 0과 1로 구성된 비트들로 나타내어지는 형태로, 작업 결과를 표시하거나 컴퓨터 메모리 주소를 저장하는 등 다양한 목적으로 사용될 수 있다. 이러한 비트 필드에서 비트 연산 등을 위해 사용하는 데이터를 비트마스크(bit mask)라고 부른다. 또한, 비트 연산을 위해 비트마스크를 활용하는 방식을 비트마스킹(bit masking)이라고 한다.

프로그래밍 문제 풀이에 있어 비트마스킹은 임의의 수와 그 비트에 관한 문제가 나왔을 때에 사용될 수 있지만, 다른 방식으로는 비트필드를 활용한 다이나믹 프로그래밍이 있다. 비트가 0과 1로 boolean처럼 참과 거짓 2개의 값만 나타낼 수 있는 점을 활용한 이 알고리즘은 정수형 2ⁿ 이내의 값을 bool array[n]과 결과로서 사용하는 방법이다. 예로 들어, {true, false, true}라는 논리형 배열이 있다고 할 때, 이를 101₂로 나타내면 (int)5라는 정수형 값만으로 긴 배열의 정보를 담을 수 있게 된다.

풀이 코드

#include <iostream>
#include <map>

using namespace std;
using lli = long long int;
// a와 b의 범위가 1e+16이므로, int로는 오버플로우 발생

int main() {
    // 자연수의 범위 a, b 입력
    lli a, b;
    cin >> a >> b;

    // 2의 거듭 제곱과 각 거듭제곱이 최상위 비트일 때의 1의 총 개수
    lli sq_two = 1;
    map<long, lli> one_count;

    // 1의 개수는 현재 값이 각각 0이면 0개, 1이면 1개
    one_count[0] = 0;
    one_count[sq_two] = sq_two;

    // 최상위 비트가 sq_two일 때, 모든 1의 개수의 누적 합
    // 즉, [1, sq_two * 2 - 1]의 범위 내에 있는 자연수들의 1의 개수 총합
    while(sq_two < b) {
        sq_two *= 2;
        one_count[sq_two] = one_count[sq_two / 2] * 2 + sq_two;
    }

    // b까지의 1의 개수와 (a - 1)까지의 1의 개수가 [a, b]의 결과
    a--;
    long long a_one = 0;
    long long b_one = 0;

    /**
     * one_count[bits / 2] := 현재 최상위 비트 이전까지의 모든 1의 개수 총합
     * (a - bits + 1) := 현재 최상위 비트를 포함하는 수들의 개수
     * 예로 들어 1100의 경우,
     * 1000~1100까지 4번 비트를 포함하는 값의 개수가 (12 - 8 + 1)개가 있다
     */
    // a 이상의 비트부터 1까지 탐색
    long long bits = 1;
    while(a > bits) bits <<= 1;
    for(; a != 0; bits >>= 1) {
        if(a & bits) {
            a_one += one_count[bits / 2] + (a - bits + 1);
            a -= bits;
        }
    }

    // b에 대해 같은 작업 수행
    bits = 1;
    while(b > bits) bits <<= 1;
    for(; b != 0; bits >>= 1) {
        if(b & bits) {
            b_one += one_count[bits / 2] + (b - bits + 1);
            b -= bits;
        }
    }

    // [a, b] 범위 내 1의 총 개수 출력
    cout << (b_one - a_one) << endl;
    return 0;
}

---