사회망 서비스(SNS)

백준 2533

GOLD III

문제 내용
해결 방안
풀이 코드

문제 내용

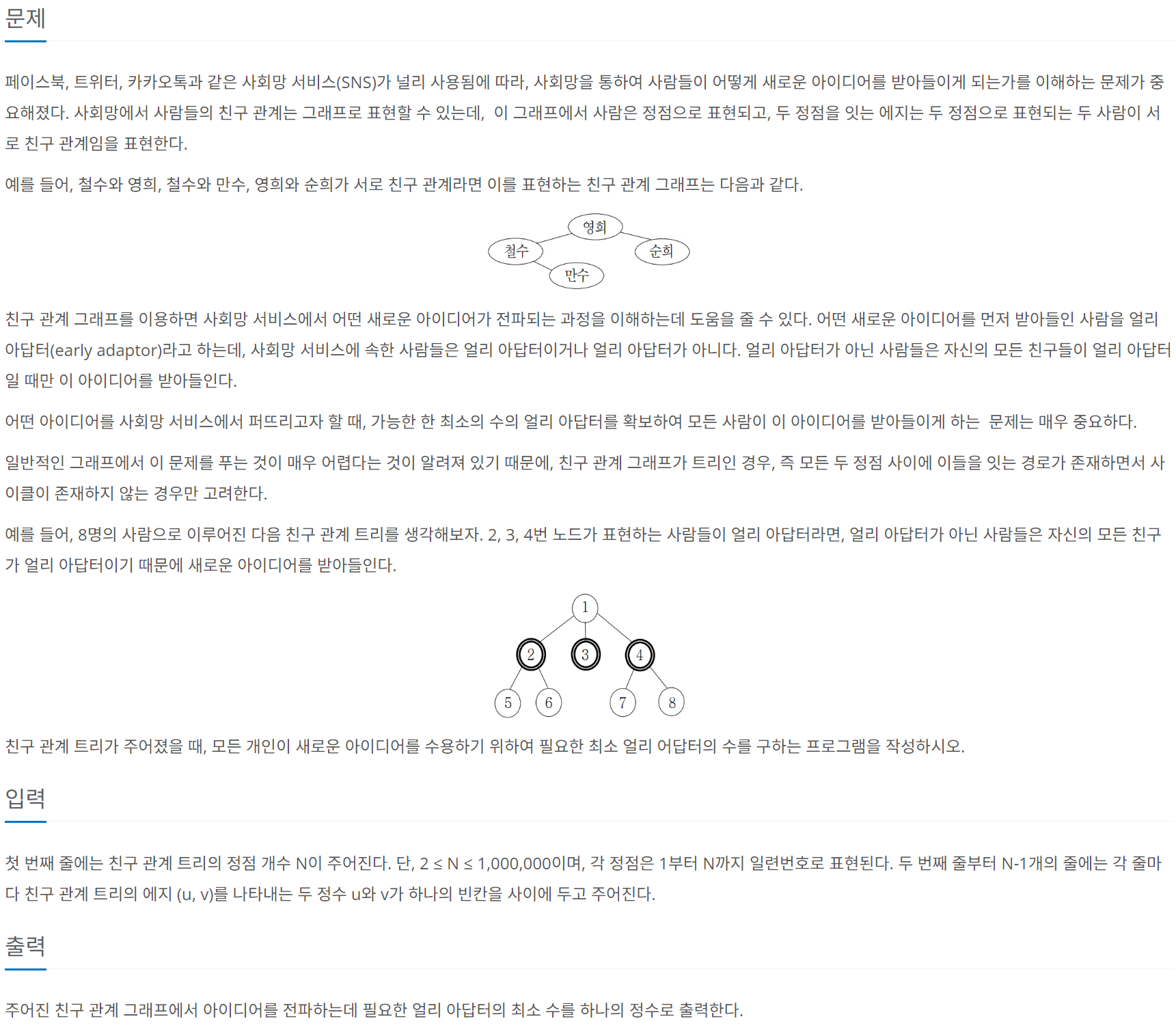
문제 링크

해결 방안

트리 구조에 대한 이해를 바탕으로 하는 문제이다. 문제에서 요구하는 바는 모든 사람이 얼리어답터나 얼리어답터와 연결된 친구 둘 중 하나의 조건을 만족할 때, 필요한 얼리어답처의 최소 인원을 구하는 문제이다. 자료구조인 트리를 기준으로 설명하면, 부모 노드나 자식 노드 둘 중 한 명 이상은 반드시 얼리어답터이어야 한다는 것이다. 우선, 문제를 풀기 위해서는 트리 구조를 만들어야 한다. 하지만 이번 문제에서는 트리 구조를 직접 구현하는 대신, 그래프에서의 인접 행렬이나 인접 리스트를 통해 문제를 해결하고자 한다.

먼저, 부모 관계로 주어지는 두 노드를 각각의 인접 리스트에 추가하고, 각 노드가 얼리어답터인 경우와 얼리어답터가 아닌 경우의 총 얼리어답터 수를 저장하는 배열을 생성한다. 그 다음, 트리의 각 리프 노드로 가서 해당 노드가 얼리어답터일 경우에는 1을 저장하고 아닌 경우에는 0을 저장한다. 이후에는 점점 부모 노드를 따라 올라가며 현재 노드와 자식 노드의 얼리어답터 여부를 비교하고 값을 수정한다. 이때, 부모 노드와 자식 노드 중에는 무조건 하나 이상이 얼리어답터이어야 하므로, 현재 노드가 얼리어답터가 아닌 경우에는 무조건 이전 노드는 얼리어답터이어야 한다. 반대로 현재 노드가 얼리어답터인 경우에는 자식 노드는 얼리어답터이거나 아닌 경우 중 더 작은 경우를 택한다. 이 과정을 루트 노드에 도달할 때까지 반복하고, 루트 노드가 얼리어답터인 경우와 아닌 경우 중 더 작은 값이 필요한 얼리어답터의 최소 인원이다.

트리(tree)란?

컴퓨터 공학에서 트리 구조(tree diagram)는 자료구조의 일종이다. 그래프와 비슷한 구조로 되어 있지만, 간선으로 이어진 각 노드 사이에는 상하관계가 있다. 각 노드의 상하 관계는 임의의 노드보다 위에 있는 부모(parent) 노드와 임의의 노드보다 아래에 있는 자식(child) 노드로 규정된다. 실제 나무처럼 최상위 부모 노드를 루트(root) 노드라고 부르고, 최하위 자식 노드를 리프(leaf) 노드라고 부른다. 간선으로 이어진 노드 사이의 거리를 깊이(depth), 전체 노드의 깊이(루트 노드와 리프 노드의 깊이)를 높이(height)라고 칭한다.

인접 행렬(adjacency matrix)란?

인접 행렬(adjacency matrix)은 각 노드와 간선으로 이어진 노드들에 대해 나타낸 행렬이다. 노드의 개수가 n인 그래프에 대한 (n × n) 행렬로, a_(ij)는 i번째 노드와 j번째 노드의 관계를 가리킨다. 유향 그래프는 a_(ij) ≠ a_(ji)이지만, 무향 그래프는 a_(ij) = a_(ji)이다. 각 행렬의 성분은 노드가 간선으로 연결되어 있는 것만 나타내는 것부터 간선의 가중치 등으로 구성된다. 노드가 간선으로 연결되어 있는 것만 나타낼 경우에는 각 노드가 가리키는 노드들을 리스트로 나타낸 인접 리스트(adjacency list) 방식도 사용할 수 있다.

풀이 코드

#include <iostream>
#include <vector>

using namespace std;

// 노드의 총 개수(친구 관계 총 인원)
int n;
// 트리에 대한 인접 리스트
vector<vector<int>> tree;
// ...[2] : 0인 경우 얼리어답터이고, 1인 경우 얼리어답터가 아님
int earlyAd[1000001][2];

// dfs를 통해 리프 노드부터 탐색
void dfs(int node) {
    // 각 노드가 얼리어답터인 경우 1을 추가하고, 아닌 경우 0으로 초기화
    earlyAd[node][0] = 1;
    earlyAd[node][1] = 0;
    
    // 인접 리스트에 연결된 모든 노드에 대해 탐색
    for(auto n: tree[node]) {
        // 만약 현재 노드가 타 노드에 의해 방문되지 않은 경우
        if(earlyAd[n][0] == -1) {
            // 해당 노드 방문
            dfs(n);
            // 현재 노드가 어답터가 아닌 경우, 연결된 노드가 얼리어답터인 경우만 취급
            earlyAd[node][1] += earlyAd[n][0];
            // 현재 노드가 어답터인 경우, 연결된 노드의 두 경우 중 최솟값 선택
            earlyAd[node][0] += min(earlyAd[n][0], earlyAd[n][1]);
        }
    }
}

int main() {
    // Fast IO
    cin.tie(0);
    cout.tie(0);
    ios_base::sync_with_stdio(false);

    // 노드의 개수 입력 및 인접 리스트 초기화
    cin >> n;
    tree = vector<vector<int>>(n + 1);

    // 각 연결된 노드들을 인접 리스트에 저장
    int u, v;
    for(int i = 0; i < n - 1; i++) {
        cin >> u >> v;
        tree[u].push_back(v);
        tree[v].push_back(u);
    }

    // 모든 노드들에 대해 방문하지 않은 것으로 간주
    for(int i = 1; i <= n; i++)
        earlyAd[i][0] = -1;

    // 루트 노드에서 시작하여 리프 노드까지 dfs로 탐색
    dfs(1);

    // 루트 노드가 얼리어답터인 경우와 아닌 경우 중 작은 값 선택
    cout << min(earlyAd[1][0], earlyAd[1][1]) << endl;
    return 0;
}