RGB거리 2

백준 17404

GOLD IV

1. 문제 내용
2. 해결 방안
3. 풀이 코드

---

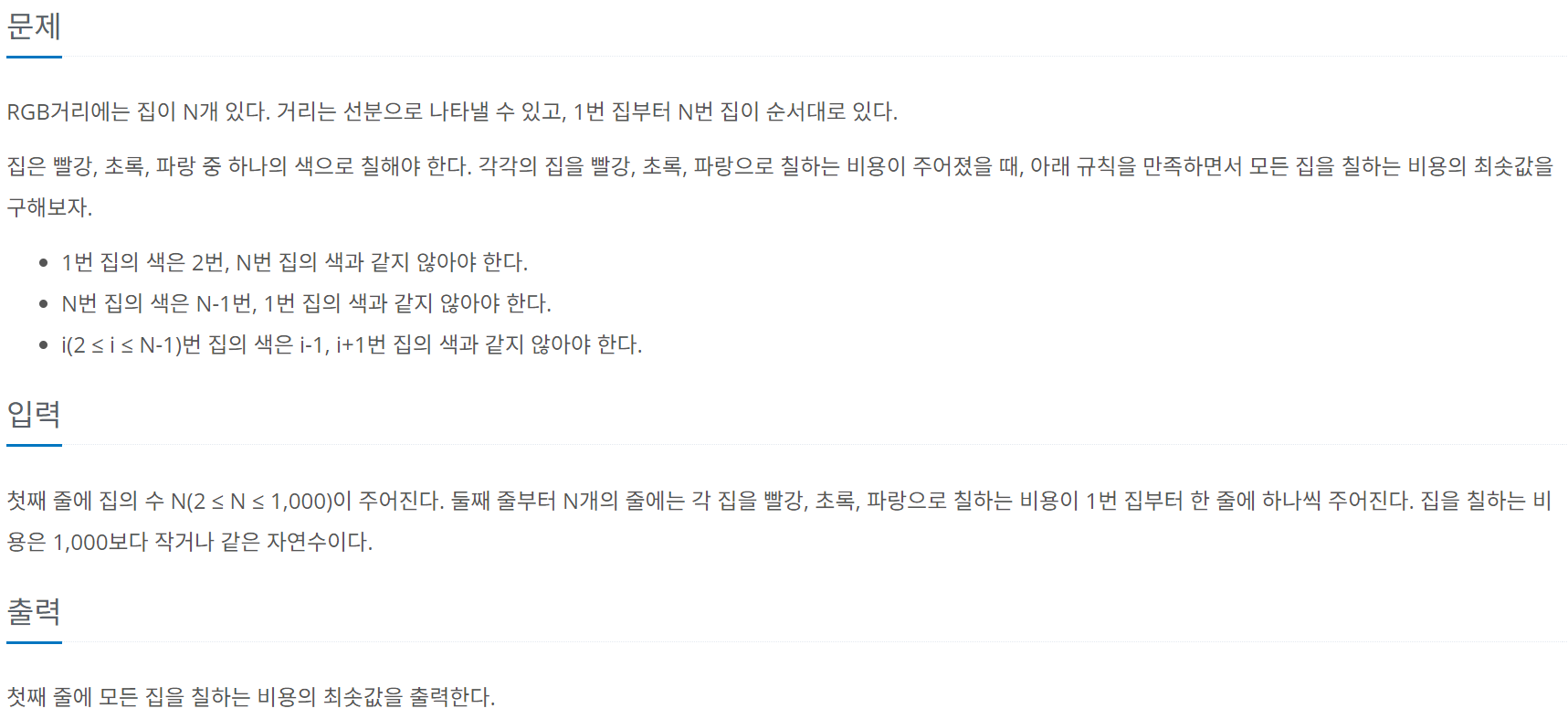
문제 내용

문제 링크

해결 방안

총 N개의 집에 빨강, 초록, 혹은 파랑 3가지 색 중에 하나의 색을 칠해야한다. 각각의 집은 자신의 앞뒤에 있는 집과 색이 달라야 한다. 예로 들어, 8번째 집은 7번째 집과 9번째 집과의 색이 달라야 한다. 추가적으로, 1번째 집과 맨 마지막 집인 N번째 집은 서로 색이 달라야 한다. 때문에 1번째 집은 2번째와 N번째, N번째 집은 (N-1)번째와 1번째 집과 색이 서로 달라야 한다. 각 집에 빨강이나 초록, 파랑 3가지 색을 칠하는 각각의 비용이 있으며, 문제에서 요구하는 바는 규칙에 따라 N개의 집에 모두 색을 칠했을 때의 드는 비용의 최솟값이다.

우선, 각 집은 자신의 이전에 있는 집과 다음에 있는 집의 색이 달라야 하는 조건을 점화식으로 생각해보자. i번째 집에 (i-1)번째 집과 (i+1)번째 집과 다른 색이 칠해져 있다고 한다면, (i+1)번째 집을 기준으로 보면 이미 i번째에는 다른 색이 칠해져 있는 것이므로 (i+2)번째 색만 고려하면 된다. 다시 말해, 임의의 집과 그 다음 집에서의 색이 다르다는 것은 그 다음 집에서 이전 집과 색이 다르다는 것과 동치라는 것이다. 때문에 각 집에 대하여 이전 집과 다른 색을 칠하기만 한다면, 임의의 집은 항상 자신의 앞뒤의 집과 다른 색을 가지는 규칙을 만족한다.

그 다음에는 1번째 집과 N번째 집과의 관계만 고려하면 된다. 인접한 집들은 자신의 이전 집과의 관계만 고려하면 되지만, 1번째와 N번째는 각각의 경우의 수를 모두 고려하는 수 밖에 없다. 1번째 집이 빨강일 때에는 N번째 집은 초록이나 파랑이어야 하고, 파랑일 때는 N번째 집은 빨강과 초록이어야 한다. 정리하자면, 각각 빨강, 파랑, 초록에서 시작한 집의 경우에는 N번째 집이 빨강, 파랑, 초록인 경우 중 시작한 집의 색깔을 제외한 경우의 최솟값을 찾으면 문제의 해답이 된다.

이제 문제를 푸는 알고리즘에 대해 알아보자. 먼저, 첫 번째 집을 빨강, 파랑, 초록으로 칠하는 경우를 각각 구분지어야 한다. 두번째 집부터 N번째 집까지는 현재 칠하려는 색과 이전에 칠해진 색을 비교하며, 이전 집에서 현재 칠하려는 색과 다른 두 색을 칠한 경우 중 총 비용이 더 적게 든 쪽을 고른다. N번째 집까지 이 과정을 반복한 후, 첫 번째 집과 N번째 집의 색이 다른 경우 중 최솟값을 찾으면 된다.

풀이 코드

#include <iostream>
#include <vector>
#define MAX_VALUE 10000

using namespace std;

int main() {
    // Fast IO
    cin.tie(0);
    cout.tie(0);
    ios_base::sync_with_stdio(false);

    int n;  // 집의 개수
    long rgb[3];  // 각 집에서의 빨강, 초록, 파랑으로 칠하는 비용

    // 1번째 집을 빨강으로 칠했을 때의 각 집에서의 빨강, 초록, 파랑으로 칠하는 최소 비용
    vector<int> rStart(3, MAX_VALUE);
    // 1번째 집을 초록으로 칠했을 때의 각 집에서의 빨강, 초록, 파랑으로 칠하는 최소 비용
    vector<int> gStart(3, MAX_VALUE);
    // 1번째 집을 파랑으로 칠했을 때의 각 집에서의 빨강, 초록, 파랑으로 칠하는 최소 비용
    vector<int> bStart(3, MAX_VALUE);
    // 각각의 칠하는 최소 비용은 처음에는 최댓값으로 시작함

    // 이전 집을 빨강, 초록, 파랑으로 칠했을 경우에 대한 각각의 총 비용
    vector<int> preValue(3);
    // 1번째 집을 빨강, 초록, 파랑으로 칠했을 때의 N번째 집에 대한 최소 비용
    int minCost[3];

    cin >> n;
    for(int i = 0; i < n; i++) {
        // 각 집을 빨강, 초록, 파랑으로 칠하는 비용 입력
        cin >> rgb[0] >> rgb[1] >> rgb[2];

        // 맨 처음 입력의 경우에는 각각 1번째 집에 칠하는 색깔의 비용만 고려한다.
        if(i == 0) {
            rStart[0] = rgb[0];
            gStart[1] = rgb[1];
            bStart[2] = rgb[2];
        }
        // 2번째부터는 현재 칠하려는 색깔과 이전 집에서 다른 색을 칠한 경우만 고려하고,
        // 그 중 최솟값을 골라 현재 칠하려는 색깔과 합한다.
        else {
            // 1번째 집이 빨강일 경우에 대한 반복
            preValue = rStart;
            rStart[0] = min(preValue[1], preValue[2]) + rgb[0];
            rStart[1] = min(preValue[0], preValue[2]) + rgb[1];
            rStart[2] = min(preValue[0], preValue[1]) + rgb[2];
            
            // 1번째 집이 초록일 경우에 대한 반복
            preValue = gStart;
            gStart[0] = min(preValue[1], preValue[2]) + rgb[0];
            gStart[1] = min(preValue[0], preValue[2]) + rgb[1];
            gStart[2] = min(preValue[0], preValue[1]) + rgb[2];
            
            // 1번째 집이 파랑일 경우에 대한 반복
            preValue = bStart;
            bStart[0] = min(preValue[1], preValue[2]) + rgb[0];
            bStart[1] = min(preValue[0], preValue[2]) + rgb[1];
            bStart[2] = min(preValue[0], preValue[1]) + rgb[2];
        }
    }

    // 1번째 집이 빨강인 경우, 마지막 집이 초록이나 파랑인 경우 중 최솟값을 취한다.
    minCost[0] = min(rStart[1], rStart[2]);
    // 1번째 집이 초록인 경우, 마지막 집이 빨강이나 파랑인 경우 중 최솟값을 취한다.
    minCost[1] = min(gStart[0], gStart[2]);
    // 1번째 집이 파랑인 경우, 마지막 집이 빨강이나 초록인 경우 중 최솟값을 취한다.
    minCost[2] = min(bStart[0], bStart[1]);

    // 1번째 집이 빨강, 초록, 파랑인 3가지 경우 중 최솟값을 찾는다.
    minCost[0] = min(minCost[0], minCost[1]);
    minCost[0] = min(minCost[0], minCost[2]);

    cout << minCost[0] << endl;
    return 0;
}

---