집으로
백준 1069
GOLD III
문제 내용
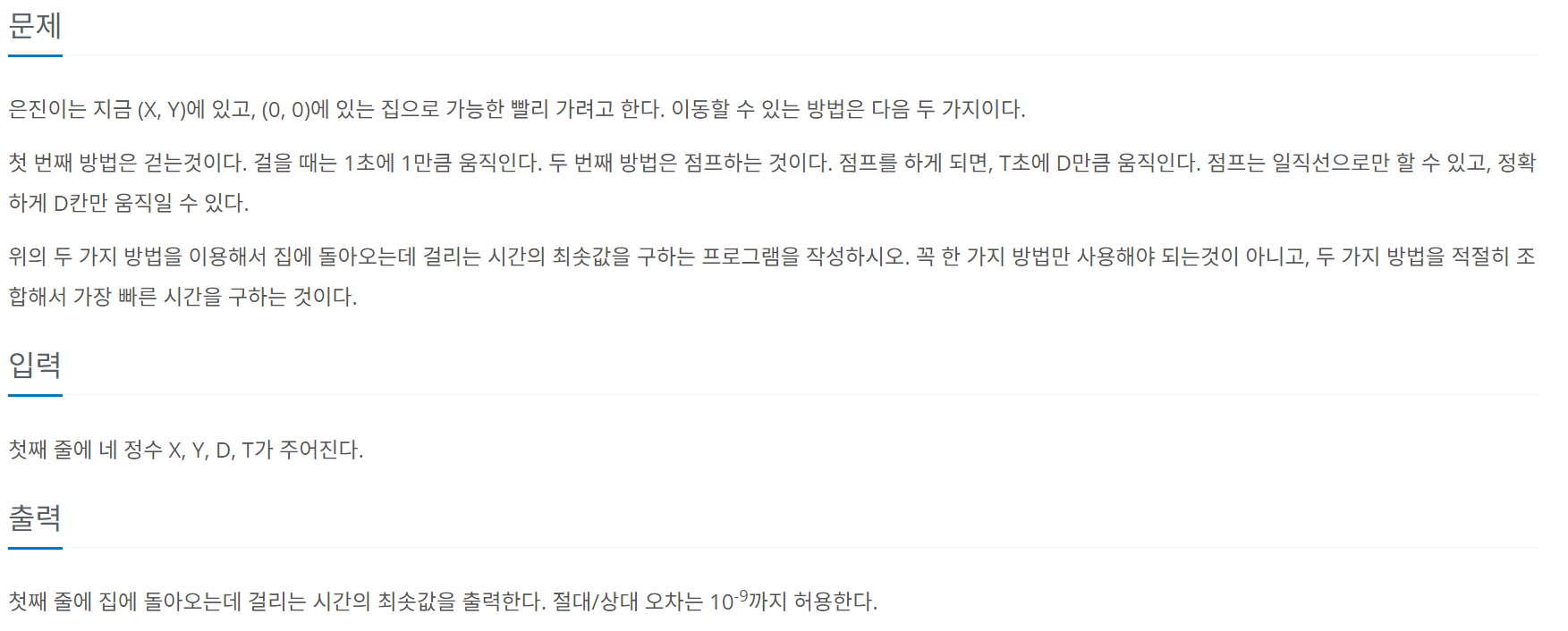
문제 링크
해결 방안
좌표 평면 위에서 원점으로 이동하는 최소 시간을 구하는 문제이다. 매초 1만큼 걷는 방법과 한 번에 한 방향으로만 반드시 d만큼 움직일 수 있는 점프를 적절히 섞어 이동할 수 있다. 걷는 것보다 점프하는 것이 더 빠르다면, 점프를 통해 크게 시간이 단축시킬 수 있으나 점프로 원점을 넘어가면 그만큼 다시 되돌아 와야 한다. 하지만 원점까지 일직선으로 가는 대신 지그재그로 가는 등의 방식으로 점프 방향을 조정하면, 점프만으로도 충분히 원점에 도달할 수 있다. 이를 위해서는 과연 점프하는 각도나 위치 등을 계산해가면서, 원점에 딱 맞게 도착하는 과정을 어떻게 정할지 고민해봐야 한다.
다시 생각해보면, 현재 문제 상황은 것은 점프가 시간 단축에 매우 유용하지만, 점프 거리가 정해져 있어 원하는 위치를 넘어가버리는 것이다. 다르게 말하면, d 이내의 거리에서 원점 방향으로 점프를 사용하는 것은 오히려 시간 단축에 불리하다는 것이다. 이를 위해 점프 각도를 조정해 정확하게 원점에 도달하는 방법을 생각해보도록 한다. 점프만으로 원점에 도착하기 위해서는 최소한 2번의 우회를 위한 점프를 해야 한다. 이 말은 즉슨, 2×d 이내의 거리의 임의의 두 좌표를 점프 2번으로 오갈 수 있는 지 판단하면 된다는 것이다.
다음 그림과 함께 살펴보자.
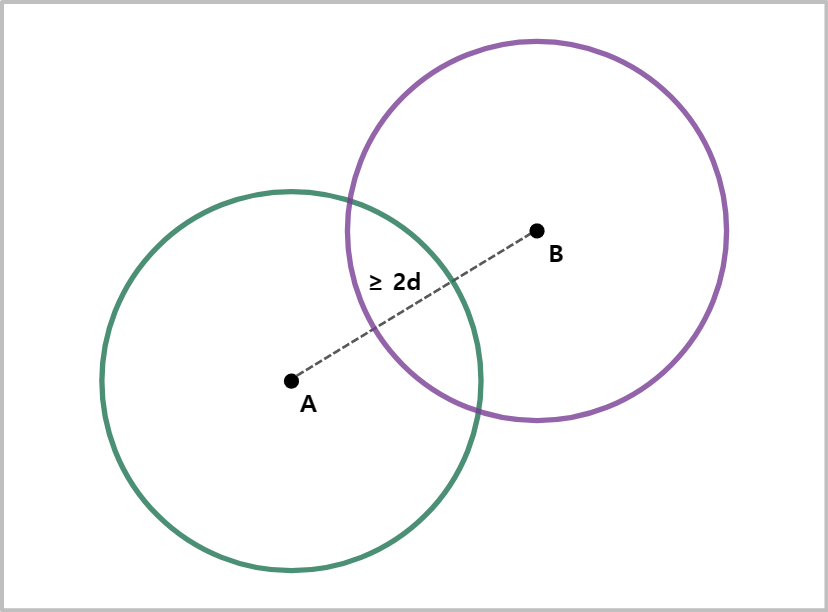
2×d 이내의 거리의 임의의 두 정점이 있다고 할 때, 각 정점에 대해 점프 가능한 거리의 자취를 그리면 원이 되는 것을 알 수 있다. 두 정점에 대해 반지름이 d인 원을 그리면 두 개의 교점이 만들어지는 것을 알 수 있다. 이 정점을 밟고 가면 두 정점을 오가는 것이 가능해진다. 거리가 정확히 2×d인 경우에는, 교점이 단 하나 생기고 그 교점은 점과 점 사이의 최단거리인 일직선 상에 존재한다. 이 것으로 우리는 2×d 이내의 거리에 있는 두 정점은 반드시 점프 2번으로 도착할 수 있다는 것을 알게 되었다.
그렇다면 우리가 목적지에 도달하는 방법은 무엇이 있을까? 결론부터 말하자면, 걷기만 하는 방법, 점프하기만 하는 방법, 걷기와 점프를 적절히 섞는 방법 총 세 가지가 있다. 만약 점프하는 것보다 걷기다 빠르다면 걷기만 하면 될 것이다. 만약 점프하는 것이 걷는 것보다 빠르다면 뛰는 방법을 우선시 할 수 있는데, 우리가 앞서 확인 했듯이 2×d 이내의 거리라면 점프 두 번만이면 충분하다. 때문에 2×d 이내의 거리까지 최단 거리인 일직선 상으로 점프하여 도착하면, 점프 2번으로 도착할 지와 d만큼 원점으로 점프한 후에 남은 거리는 걸어갈 지를 선택할 수 있다. 이러한 총 세 가지 방법 중 각각에 대해 계산한 뒤 최솟값을 고르면 답이 간단하게 나올 것이다.
풀이 코드
#include <iostream>
#include <cmath>
using namespace std;
// 세 값 중 최솟값 선택
double Min(double walk, double wnj, double jump) {
double min_result = walk;
min_result = min(min_result, wnj);
min_result = min(min_result, jump);
return min_result;
}
int main() {
// 현재 위치 x, y와 점프 거리 d, 점프 시간 t 입력
long long x, y, d, t;
cin >> x >> y >> d >> t;
// 소숫점 12자리로 고정
cout.precision(12);
cout << fixed;
// 현재 위치로부터 원점까지의 거리
double distance = sqrt(x * x + y * y);
// 만약 현재 거리가 점프 거리보다 멀다면
if(distance >= d) {
// 점프해야 하는 횟수
long long jump = distance / d;
// 걷기만 하거나, d 이내의 거리까지 점프하고 나머지는 걷거나,
// 2×d 이내의 거리에서 두 번 점프하기
cout << Min(distance, jump * t + (distance - (jump * d)), (jump + 1) * t);
}
// 만약 현재 거리가 d 이내라면
else {
// 걷기만 하거나, 원점을 넘어 뛰고 걸어서 돌아가거나,
// 2×d 이내의 거리에서 두 번 점프하기
cout << Min(distance, t + (d - distance), 2 * t);
}
return 0;
}