두 포인터(Two Pointer)
두 포인터란?
두 포인터는 임의의 리스트에 대해 각 인덱스를 가리키는 두 개의 포인터로, 조건을 만족할 때까지 반복하여 포인터를 움직이는 풀이 방식이다. 두 포인터는 알고리즘으로 분류되기 보다는 문제를 해결하는 기술이나 방법에 가깝지만, 문제를 접근하는 데에 도움이 되기 때문에 알고리즘으로 작성하기로 하였다.
예제 코드
아래의 코드는 백준 2470번: 두 용액의 해답 코드이다.
해당 문제를 간략히 설명하면, 0이 아닌 정수로 이루어진 임의의 리스트의 두 원소의 합이 0에 가장 가까운 원소쌍을 찾는 문제이다.
#include <iostream>
#include <algorithm>
#define INF 2 * 1e9 + 1
using namespace std;
// 용액의 개수 (n≡{x:2≤x≤100,000})
int n;
// 용액의 특성값 (arr≡{x:-1e9≤x≤1e9,x≠0})
int arr[100000];
int main() {
// Fast I/O
cin.tie(0);
ios_base::sync_with_stdio(false);
// 용액의 개수와 그 특성값 입력
cin >> n;
for(int i = 0; i < n; i++)
cin >> arr[i];
// 용액을 오름차순으로 정렬
sort(arr, arr + n);
// 용액의 최솟값 비교를 위한 임의의 큰 수 지정
int min_attr = INF;
// 결과 출력을 위한 변수
int min_result, max_result;
// 두 포인터의 두 인덱스 지정
int left = 0;
int right = n - 1;
// 두 포인터가 만나기 전까지 반복
while(left < right) {
// 두 용액의 혼합 특성값의 절댓값
int attr = abs(arr[left] + arr[right]);
// 만약 현재 혼합 특성값이 가장 작다면,
// 최솟값 갱신 및 결과 출력을 위한 값 저장
if(min_attr > attr) {
min_attr = attr;
min_result = arr[left];
max_result = arr[right];
}
// 두 용액의 절댓값 차이가 작아지는 방향으로 포인터 이동
if(abs(arr[left]) > abs(arr[right]))
left++;
else
right--;
}
// 최솟값에 해당하는 두 용액의 특성값 출력
cout << min_result << ' ' << max_result << endl;
return 0;
}
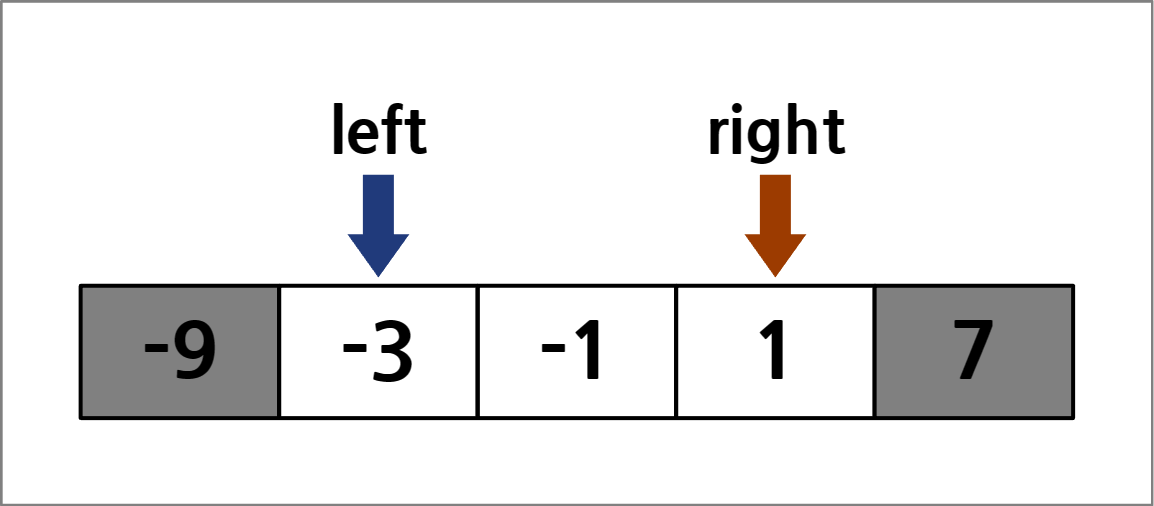
코드의 내용을 요약하자면, 주어진 배열을 오름차순으로 정렬하고 두 포인터를 사용해 조건에 맞는 원소쌍을 찾는다. 만약 왼쪽의 포인터가 가리키는 값의 절댓값이 더 크다면 왼쪽의 포인터를 오른쪽으로 움직이고, 반대로 오른쪽의 포인터가 가리키는 값의 절댓값이 더 크다면 오른쪽의 포인터를 왼쪽으로 움직인다. 이 과정을 그림으로 나타내면 다음과 같다.

음수는 왼쪽에 위치한 값이 오른쪽에 위치한 값보다 절댓값이 크므로 오른쪽으로 움직이고, 양수는 오른쪽에 위치한 값이 왼쪽에 위치한 값보다 절댓값이 크므로 왼쪽으로 움직인다. 두 포인터의 값의 부호가 다를 경우에는 절댓값이 작아져야 두 수의 절댓값 차이도 작아질 수 있으므로, 절댓값이 작아지는 방향으로 이동한다.
이처럼 임의의 두 인덱스나 구간을 지정할 때에 모든 범위를 순회하는 대신 두 개의 포인터로 조건을 만족하는 일부만 확인하는 방식을 두 포인터라고 한다.
두 포인터의 특징
위의 예제 문제를 다시 한 번 예로 들어보자. 위의 문제를 해결하기 위한 방법 중 브루트포스로 접근했다고 가정한다면, 차이가 최소인 두 원소쌍을 찾기 위해 모든 인덱스에 대해 순회해야 할 것이다. 이를 이중 반복문을 통해 구현하면, 최대 연산 횟수는 N(N - 1)이므로 시간 복잡도는 O(N²)가 나온다.
하지만, 위의 방식대로 두 포인터를 사용하여 풀이한다면, 최대 연산 횟수는 왼쪽 포인터와 오른쪽 포인터가 모두 N이므로 시간 복잡도 O(N)만에 해결하는 것이 가능하다. O(N²)과 O(N)은 리스트의 길이인 N이 커질수록 연산 횟수와 소요 시간은 극명하게 차이가 난다. 즉, 브루트포스 방식을 통한 반복문보다 두 포인터를 사용하는 방식은 시간 복잡도에 있어 이점을 가진다.
앞서 말했듯 두 포인터는 문제 풀이에 있어 중요한 시간 복잡도에서 단순 반복보다 큰 우위를 지닌다. 때문에, 임의의 인덱스나 구간을 찾는 문제들을 모두 반복문 대신 두 포인터로 해결하면 된다는 생각이 들 수 있다. 비교를 위해 두 문제를 가져왔다.
소수의 연속합(1644번) 문제는 두 포인터를 사용하여 구간의 연속합이 작으면 구간을 늘리고 구간의 연속합이 크면 구간을 줄이는 방식으로 정답을 찾는 두 포인터 문제이다. 하지만, 연속합(1912번) 문제는 조건도 간단하고 난이도도 쉽지만, 두 포인터를 사용하여 풀 수 없는 문제이다. 난이도와 무관하게 두 포인터의 사용 여부를 결정짓는 것은 탐색 조건과 리스트의 규칙성이다. 앞서 말한 두 포인터의 정의를 다시 한 번 살펴보자.
두 포인터는 임의의 리스트에 대해 각 인덱스를 가리키는 두 개의 포인터로, 조건을 만족할 때까지 반복하여 포인터를 움직이는 풀이 방식이다.
여기서 중요한 것은 만족해야할 조건, 그리고 조건을 만족하기 위해 포인터가 움직이는 방향인 리스트의 규칙성이다. 소수의 연속합(1644번) 문제는 연속된 소수의 합으로 만들어야 하는 자연수라는 조건이 명시되어 있고, 뒤로 갈수록 소수가 증가하는 오름차순으로 되어있기에 리스트의 규칙성도 만족하는 상황이다. 때문에, 연속된 소수의 합이 크면 구간을 줄이고, 반대로 크면 구간을 늘리는 과정을 반복하면 해결할 수 있다. 반대로 연속합(1912번) 문제는 가장 큰 합이라는 불명확한 조건과 음수와 양수가 임의로 섞인 리스트라는 점에서 포인터를 배치하기 모호한 방향으로 인해 반복문을 통해 처리하는 것이 더 적합하다.
다만, 리스트가 정렬되어 있지 않다는 것이 리스트의 규칙성을 만족하지 못한다고 오해해서는 안된다. 그 예시로, 백준 1806번: 부분합 문제가 있다. 문제를 간략히 설명하면, 정렬되지 않은 자연수들로 되어있는 리스트에서 합이 일정 값 이상인 최소 길이의 부분합을 찾는 문제이다. 부분합의 최솟값이라는 조건이 명시되어 있지만, 정렬되어 있지 않아 리스트의 규칙성을 만족하지 못한다고 생각할 수 있다. 하지만, 모든 원소가 자연수라는 점에서 부분합은 구간이 늘어날수록 반드시 증가하는 방향이기 떄문에, 부분합의 최솟값을 만족하는 지에 따라 구간을 조절하며 조건을 만족하는 구간의 길이 중 최소 길이를 찾으면 된다.
두 포인터를 사용하면 브루트포스나 단순 반복을 사용하는 것보다 시간 복잡도에서 이점을 가진다. 그러나, 두 포인터를 사용하기 위해서는 문제의 탐색 조건이 명확해야하며, 포인터가 이동해야할 방향인 리스트의 규칙성이 보장되어야 한다.
슬라이딩 윈도우(Sliding Window)
해당 글을 작성하던 중에 알게된 점이지만, 두 포인터의 종류로 슬라이딩 윈도우라는 방식이 있다고 한다. 간단히 설명하면, 구간을 지정하는 두 포인터 중 그 구간을 일정하게 하는 방식를 말한다. 리스트의 길이를 N, 구간을 M이라고 한다면, 반복문으로 작동하면 O(NM)의 시간 복잡도가 나온다. 하지만, 슬라이딩 윈도우를 사용하면 O(N)으로 해결하는 것이 가능하다.
그 예시로 백준 21921번: 블로그 문제를 들 수 있다. 단순 반복문을 쓰게 되면 최대 2*1e9만큼의 연산량이 나와 시간 내에 처리할 수 없다. 슬라이딩 윈도우 방식을 사용하면, 구간을 한 칸 이동할 때마다 앞의 인덱스의 값을 더하고 뒤의 인덱스의 값만 빼주면 되므로 연산량이 크게 줄어든다. 아래는 그 풀이에 대한 코드이다.
#include <iostream>
using namespace std;
int main() {
// Fast I/O
cin.tie(0);
ios_base::sync_with_stdio(false);
// 블로그 총 일 수와 탐색 구간
int n, x;
// 블로그 일 별 방문자 수
int visit[250001];
// 구간 x에서의 방문자 합
int x_visit = 0;
// 블로그 일 수 및 구간 입력
cin >> n >> x;
// x일까지의 블로그 방문자 수와 구간 내 방문자 합 저장
for(int i = 0; i < x; i++) {
cin >> visit[i];
x_visit += visit[i];
}
// 구간 내 최고 방문자 수와 그 구간의 개수 저장
int max_visit = x_visit;
int max_count = 1;
// x일부터 n일까지의 방문자 확인
for(int i = x; i < n; i++) {
// 당일 방문자 수 입력
cin >> visit[i];
// 구간의 길이를 유지하면서 당일의 방문자 합산
x_visit += visit[i];
x_visit -= visit[i - x];
// 구간 내 방문자 수가 최대일 경우, 일 수나 최댓값을 갱신
if(max_visit == x_visit)
max_count++;
else if(max_visit < x_visit) {
max_visit = x_visit;
max_count = 1;
}
}
// 블로그 방문자가 없을 때의 예외 처리
// 방문자가 있다면 그 최댓값과 일 수를 출력
if(max_visit == 0)
cout << "SAD\n";
else
cout << max_visit << '\n' << max_count << '\n';
return 0;
}