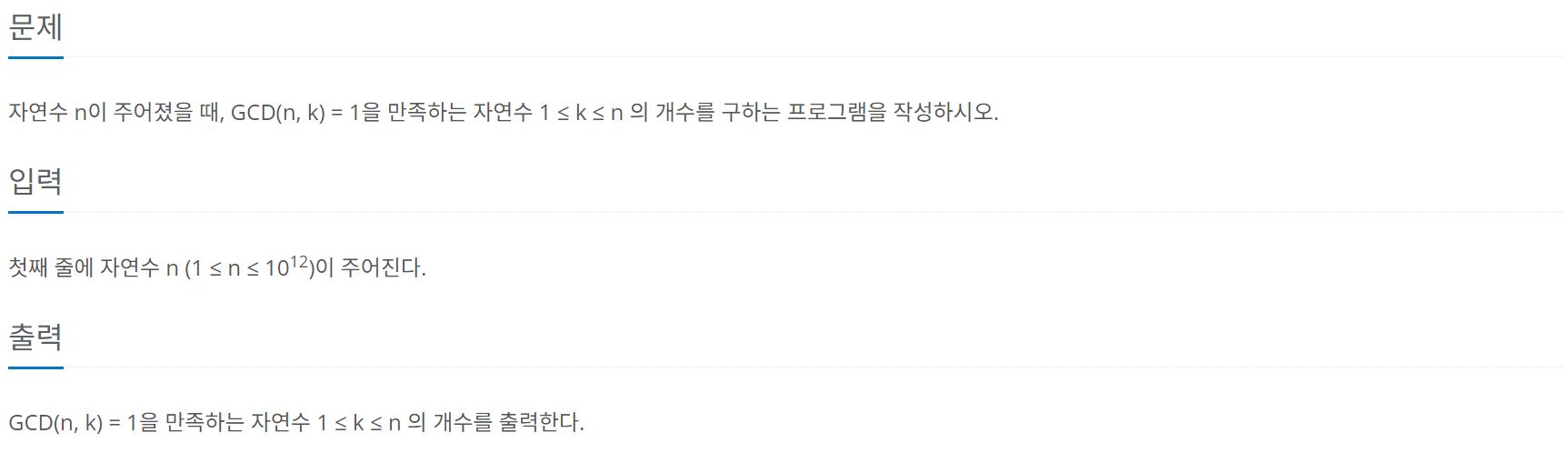
GCD(n, k) = 1

백준 11689

GOLD I

1. 문제 내용
2. 해결 방안
3. 풀이 코드

---

문제 내용

문제 링크

해결 방안

문제는 너무나도 간단하다. n의 값을 입력받아 [1, n]의 범위에서 n과의 공약수가 1인, 즉 서로소의 개수를 찾으면 된다. 수학 관련 문제를 어느 정도 풀어봤다면, 공약수와 관련된 문제라는 점에서 유클리드 호제법과 같은 관련 수식들을 떠올릴 수 있을 것이다. 그러나, 유클리드 호제법으로 풀었을 경우부터 이야기하자면, 유클리드 호제법의 시간복잡도는 O(log₂(min(a, b)))이므로 이 문제에서 주어진 정보에 따르면 O(log₂k)이다. 그리고 이를 [1, n]까지 탐색해야하므로, 결과적으로 유클리드 호제법으로 풀면 O(nlog₂k)의 시간복잡도를 가진다. 주어진 n의 범위가 1 ≤ n ≤ 1e+12이기 때문에, 유클리드 호제법 등을 사용한 브루트포스로 풀기에는 무리가 있다.

다행히도 문제에서 요구하는 n과 서로소인 n 이하의 자연수의 개수를 특수함수인 오일러 피 함수가 있다. 오일러 피 함수의 각 성질을 사용하면, 임의의 수를 소인수분해한 결과를 통해 해당 수의 오일러 피 함수의 값을 찾을 수 있다. 임의의 수를 소인수분해하면, 소수의 거듭제곱에 대한 여러 곱들로 나타내어진다. 각 소수는 pⁿ(1 - 1/p)꼴로 나타내어지고, 이 중 pⁿ의 곱은 오일러 피 함수에서의 매개변수를 소인수분해한 값이다. 다시 말해, 소인수분해한 소인수들의 (1 - 1/p) 또는 (p - 1)/p 꼴의 곱을 오일러 피 함수의 매개변수와 곱하면, 오일러 피 함수의 값이 나온다. 이 값은 곧 문제에서 요구하는 임의의 자연수 이하의 서로소인 자연수들의 개수와 같다.

오일러 피 함수(euler phi function)란?

오일러 피 함수 혹은 오일러 파이 함수라고도 불리는 이 함수는 φ(n)라고 쓴다.

수식으로 나타내자면, 로, 오일러 피 함수란 자연수 n과 최대공약수가 1인 n과 서로소인 n 이하의 자연수의 개수이다.

오일러 피 함수는 곱셈적 함수이기 때문에, 서로소인 자연수 a, b에 대해 φ(ab) = φ(a)φ(b)가 성립한다. 또한, 임의의 소수 p에 대해 φ(pⁿ) = pⁿ(1 - 1/p)가 성립한다. p^n의 약수는 1과 p의 배수 뿐이고 p^n개의 수 중 p의 배수는 총 p^(n-1)개 있으므로, 결론적으로 φ(p^n) = p^n - p^(n-1) = p^n(1 - 1/p)가 된다.

풀이 코드

#include <iostream>

using namespace std;

int main() {
    // 오일러 피 함수의 매개변수
    long long n;
    cin >> n;

    // 소인수의 오일러 피 함수 값들의 곱 중 pⁿ 꼴의 곱은 n이다.
    long long euler = n;
    // [2, √n]의 범위 내에 있는 자연수 중 소인수를 찾는다.
    for(long long p = 2; p * p <= n; p++) {
        // p가 n의 소인수일 경우, n에 소인수의 (p-1)/p를 곱한다.
        if(n % p == 0)
            euler = euler / p * (p - 1);
        // 소인수의 거듭제곱(pⁿ)은 이미 n만큼 곱했으므로, p의 거듭제곱을 지운다.
        while(n % p == 0)
            n /= p;
    }

    // 가장 큰 소수가 거듭제곱으로 이루어져 1이 될 때까지 나눠진 경우,
    // 오일러 피 함수를 그대로 출력한다.
    if(n == 1)
        cout << euler << endl;
    // 가장 큰 소수가 거듭제곱이 아니어서 위 과정에서 가장 큰 소수가 남은 경우, 
    // 남은 마지막 수에 대해 소수에 대한 오일러 피 함수의 곱셈을 계산하여 출력한다.
    else
        cout << (euler / n * (n - 1)) << endl;
    return 0;
}

---