줄 세우기

백준 2252

GOLD III

문제 내용
해결 방안
풀이 코드

문제 내용

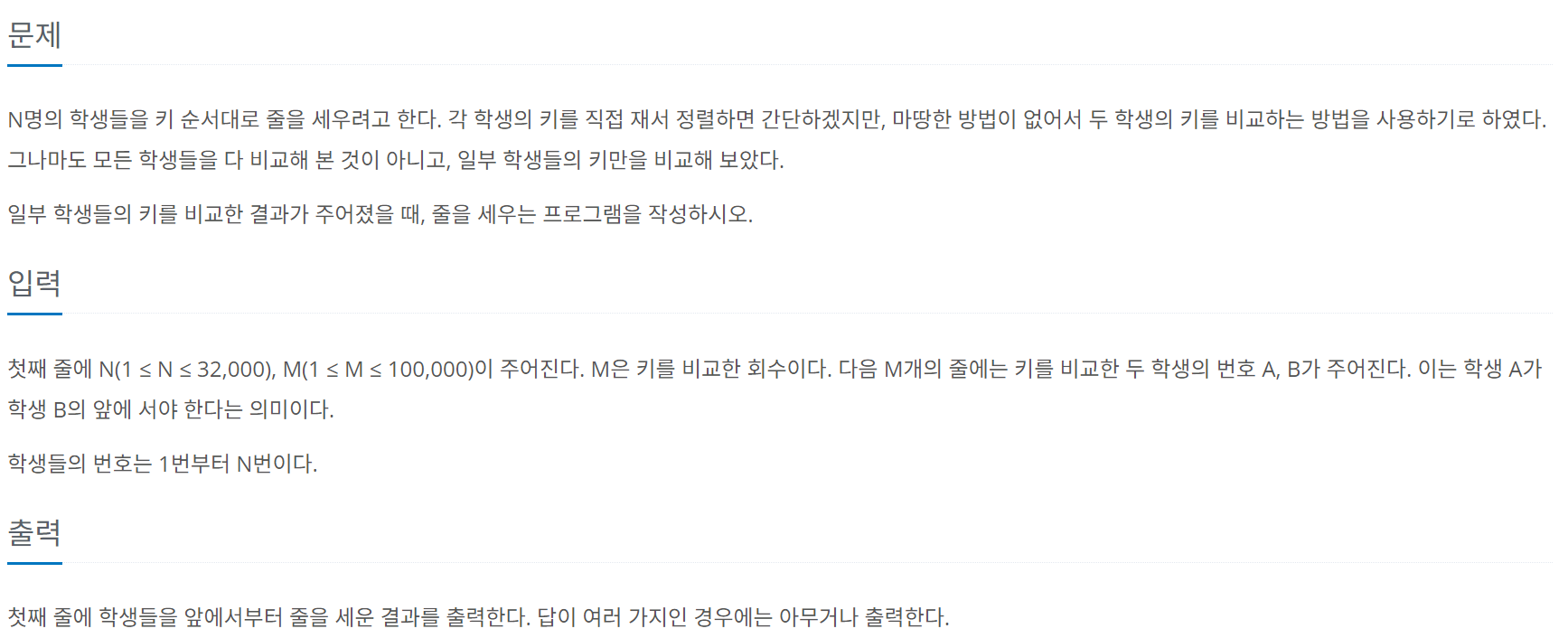
문제 링크

해결 방안

문제에 따르면, N명의 학생들 중 일부 학생들에 대하여 학생 두 명씩 줄을 서는 순서만이 주어진 상태이다. 간단히 말하자면, 첫째 줄을 제외한 임의의 줄에서 A B라는 정보가 주어지면, 줄을 설 때 A가 B의 앞에만 있으면 된다. 결과적으로 임의의 줄에서 나타난 순서에 위배만 되지 않는다면 순서를 어떻게 세우든 상관없다. 각각 두 학생들 사이에 방향성이 있고 줄에 순환이 없으므로, 이 문제는 위상 정렬로 풀 수 있다.

먼저, 위상 정렬을 위해 각 학생들의 앞에 나와야 하는 학생들의 수를 확인한다. 그리고, 앞에 나오는 다른 학생들이 없는 학생들을 먼저 앞에 세운다. 각 학생들이 앞에 나오면, 해당 학생들 뒤에 나와야 하는 학생들을 이어서 세운다. 이 과정을 반복하면, 주어진 순서 정보를 따르는 방향으로 학생들이 정렬된다.

위상 정렬(topological sort)이란?

유향 비순환 그래프(Directed Acyclic Graph; DAG)의 방향성을 따라 순서대로 배열하는 정렬 방식이다. 다양한 정렬 알고리즘이 존재하지만, 대표적으로 Kahn’s algorithm(for topological sort)이 있다.

Kahn’s algorithm의 순서는 다음과 같다.

각 노드로 향하는 간선의 개수를 조사하여, 노드로 향하는 간선의 개수가 0인 노드들을 찾는다.

찾은 노드들을 하나씩 꺼내, 해당 노드의 간선들이 가리키는 노드의 간선의 개수를 하나씩 줄인다.

만약 노드로 향하는 간선의 개수가 0인 노드가 발생하면, 해당 노드도 찾은 노드 목록에 추가한다.

모든 노드들을 찾아 간선들을 확인할 때까지 이 과정을 반복한다.

유향 비순환 그래프(Directed Acyclic Graph)이란?

유향 비순환 그래프(Directed Acyclic Graph; DAG)는 풀어서 설명하자면, 방향이 있고 순환하지 않는 그래프이다. 노드와 노드 사이의 간선에 방향성이 있어, 해당 방향성을 위배하지 않는 선에서 두 노드가 이어져있다. 그리고 비순환이라는 말에서 알 수 있듯이, 이러한 방향을 따라갔을 때 어느 출발 지점으로 돌아오는 간선이 존재해서는 안 된다. 예로 들어 A에서 B를 향하는 간선(A→B)가 있다고 한다면, B에서 A로 이동하는 것은 방향성에 위배되기 때문에 불가능하다. 또한, (A→B)와 (B→C)라는 간선이 있을 때, (C→A)라는 간선은 순환(cycle)이 만들어지기 때문에 존재할 수 없다.

풀이 코드

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

int main() {
    int n, m;  // 학생들의 수와 순서쌍의 수
    int a, b;  // 학생들의 순서쌍
    vector<vector<int>> table(n + 1);  // 인덱스별 자신의 뒤에 나오는 학생 리스트
    vector<int> priority(n + 1);  // 인덱스별 자신의 앞에 나오는 학생들의 수
    queue<int> q;  // 앞에 서는 순서
    int top;  // 현재 줄을 서는 학생

    cin >> n >> m;
    for(int i = 0; i < m; i++) {
        cin >> a >> b;
        // 앞에 나오는 학생들이 뒤에 나오는 학생들의 명단을 가진다.
        table[a].push_back(b);
        // 뒤에 나오는 학생들은 자신의 앞에 나오는 학생들의 수를 기록한다.
        priority[b]++;
    }

    // 자신의 앞에 서는 학생이 없는 학생들을 먼저 큐(queue)에 넣는다.
    for(int i = 1; i <= n; i++) {
        if(priority[i] == 0)
            q.push(i);
    }

    while(!q.empty()) {
        // 큐에서 나오는 순서대로 학생들을 출력한다.
        top = q.front();
        q.pop();
        cout << top << ' ';

        // 먼저 나온 학생들은 뒤에 나오는 학생들의 '앞에 나오는 학생 수'를 감소시킨다.
        // '앞에 나오는 학생 수'가 0이 되면, 그 학생도 이어서 줄을 선다.
        for(auto node: table[top]) {
            priority[node]--;
            if(priority[node] == 0)
                q.push(node);
        }
    }
    cout << endl;
    return 0;
}