가장 긴 증가하는 부분 수열 5
백준 14003
PLATINUM V
문제 내용
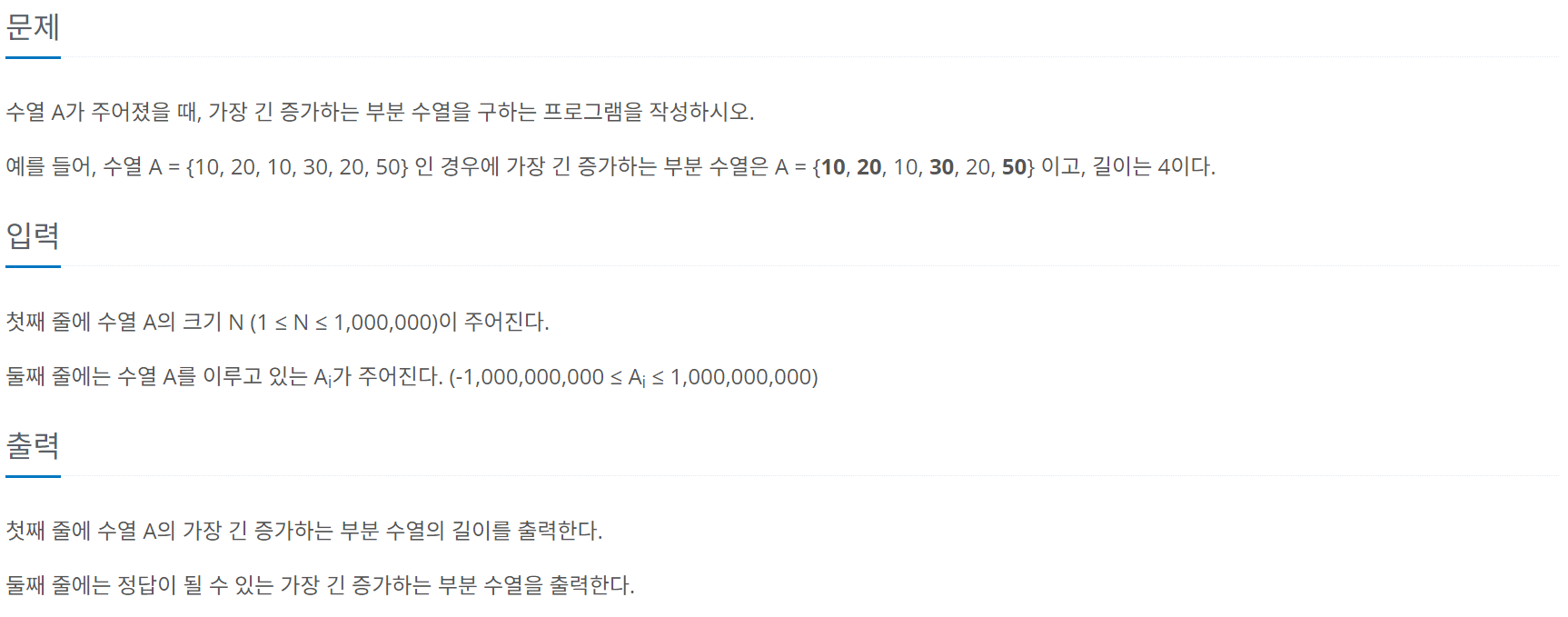
문제 링크
해결 방안
임의의 음수와 양수로 이루어진 수열에 대한 최장 증가 부분 수열(LIS)을 찾고, 그 길이와 그 길이를 가진 증가 부분 수열을 출력하면 된다. 최장 증가 부분 수열의 최적화된 풀이를 위해, 바텀 업 방식와 메모이제이션을 활용한 다이나믹 프로그래밍으로 해결해야 한다.
우선, 수열의 길이와 수열의 각 원소를 입력받는다. 수열의 첫 원소는 그대로 최장 증가 부분 수열에 포함시켜 주면 된다. 수열의 두번째 원소부터는 각 원소가 증가 부분 수열의 가장 마지막 원소일 경우들을 고려해야 하는데, 각 원소가 증가 부분 수열의 가장 마지막 원소이기 위해서는 현재 원소가 이전 원소보다 커야한다. 이번 문제에서 찾고자 하는 것이 최장 증가 부분 수열이므로 현재 원소보다 작은 이전 원소들이 가장 많은 경우를 고려해야 한다. 이를 위해, 현재 원소보다 작은 원소가 처음으로 나올 때까지 이전의 원소들을 되짚어가며 찾고, 처음으로 작은 값이 있는 인덱스의 바로 다음 위치에 삽입하면 해당 위치까지가 현재 원소에 대한 최장 증가 부분 수열이다. 이 과정을 모든 원소에 대해 실행하는 대신, 메모이제이션을 활용하여 찾게 되면 연산 횟수를 줄일 수 있다. 방법을 간단하게 설명하자면, 입력받은 원소와 메모이제이션된 최장 증가 부분 수열의 각 원소들을 비교하고 현재 원소보다 작은 원소 바로 다음 원소를 현재 원소로 대체한다. 대체되는 원소가 현재 원소보다 작으면, 현재 원소는 그 원소 다음에 위치할 것이므로 대체되는 원소는 항상 현재 원소보다 항상 크거나 같다. 때문에, 이후 나오는 원소들은 더 작은 값으로 대체된 원소로 인해 증가 부분 수열의 뒤에 위치할 가능성이 커지게 된다. 메모이제이션을 활용하는 상세한 알고리즘과 풀이 과정은 각 링크를 통해 확인하기를 권장한다.
하지만, 이러한 방법을 사용하더라도 모든 원소에 대해 시행하는 것보다 시간은 단축되겠지만, 메모이제이션한 수열을 찾는 과정도 결국 O(N)이기 때문에 결과에 대한 시간복잡도는 O(N²)이다. 때문에 메모이제이션한 원소 중에서 현재 원소가 들어갈 위치를 찾는 과정도 최적화할 필요가 있는데, 다행히도 메모이제이션한 원소들은 증가 부분 수열의 원소이기 때문에 오름차순으로 정렬되어 있다. 여기서 우리는 lower bound라는 이진 탐색 기법을 사용할 것이다. 각 원소를 이진 탐색처럼 두 부분으로 나누어 탐색하되, 검색 기준은 원하는 숫자가 아닌 원하는 숫자보다 작지 않은 값이 처음으로 나오는 부분이 된다. lower bound를 이용하여 최장 증가 부분 수열을 찾는 알고리즘의 코드 풀이는 링크에 보다 잘 설명되어 있으니 확인하기 바란다.
마지막으로, 가장 긴 부분 수열을 출력해야 하므로, 증가 부분 수열을 만드는 과정에서 각 원소의 증가 부분 수열에서의 위치를 기록해야 한다. 모든 원소에 대해 부분 증가 수열을 만든 뒤에는 최장 증가 부분 수열의 마지막 원소부터 시작하여, 이전 인덱스로 돌아가며 길이가 최장 길이부터 각 1씩 감소한 원소들을 찾으면 된다. 실제로 어떤 원소로 최장 증가 부분 수열을 찾았든지에 관계 없이, 최장 증가 부분 수열이 될 수 있는 결과만 찾으면 되므로 그리디 알고리즘을 통해 찾는다. 그리고 찾은 원소들을 역순으로 출력하면 주어진 수열에 대한 최장 증가 부분 수열이 완성된다.
결과적으로 이번 문제의 시간복잡도는 최장 증가 부분 수열을 찾는 과정이 O(Nlog₂N)이고 역순으로 최장 증가 부분 수열을 만드는 과정이 O(N)이므로, 최종적으로는 O(Nlog₂N)에 O(N)을 합한 O(N(log₂N + 1)) = O(Nlog₂N)이다.
최장 증가 부분 수열(Longest Increasing Subsequence; LIS)이란?
최장 증가 부분 수열(Longest Increasing Subsequence; LIS)은 각 수열의 원소가 증가하는 부분 수열 중 가장 긴 수열을 의미한다. 다시 말해, 부분 수열의 길이를 넘지 않는 임의의 자연수 i < j에 대해, 부분 수열의 i번째 원소는 j번째 원소보다 작거나 같지 않다는 조건을 만족하는 원소들로만 이루어진 부분 수열을 증가 부분 수열이라고 한다. 최장 증가 부분 수열은 주어진 수열의 모든 증가 부분 수열 중 수열의 길이가 가장 긴 부분 수열을 의미한다. 최장 증가 부분 수열을 찾는 가장 간단한 알고리즘은 수열의 모든 원소들로부터 이전 인덱스들로 돌아가며 찾는 방법이 있으나, 이 경우에는 시간복잡도가 O(N²)가 나오게 된다. 이 방법은 수열의 길이가 길어질수록 시간이 너무 많이 걸리게 되므로, 이번 문제에서는 O(Nlog₂N)으로 해결할 수 있는 최적화된 풀이에 대해 설명한다.
이진 탐색(binary search)이란?
이진 탐색(binary search)은 정렬된 리스트에 대해 검색 범위를 줄여나가며 원하는 데이터를 찾는 알고리즘이다. 정렬된 원소들은 임의의 원소에 대해 대소 관계가 정렬 기준과 같기 때문에, 각 원소들을 대소 관계에 따라 두 부분으로 나누어 탐색한다. 가운데의 원소가 찾고자 하는 값보다 클 때와 작을 때를 구분하여, 각 대소 관계에 따라 나눈 두 부분으로 검색 범위를 좁히고 해당 부분에 대해 다시 두 부분으로 나누어 탐색을 진행한다. 원하는 원소를 찾거나 더 이상 원소를 찾을 수 없을 때까지 계속 두 부분으로 나누어 탐색하기에 이진 탐색이라고 불린다. 2ⁿ 이하의 크기를 가진 리스트는 최대 n번으로 원소를 찾을 수 있기 때문에, 시간복잡도가 O(log₂N)이 나온다.
풀이 코드
#include <iostream>
#include <vector>
using namespace std;
// 수열의 각 원소들을 저장하는 배열
long permut[1000000];
// 현재의 최장 증가 부분 수열을 저장하는 배열
long lis[1000000];
// 수열의 각 원소들의 최장 증가 부분 수열의 인덱스를 저장하는 배열
int memo[1000000];
int main() {
// Fast IO
cin.tie(0);
cout.tie(0);
ios_base::sync_with_stdio(false);
// 수열의 크기 입력
int n;
cin >> n;
// 최장 증가 부분 수열의 인덱스 초기화
int index = 0;
for(int i = 0; i < n; i++) {
// 수열의 각 원소 입력
cin >> permut[i];
// 증가 부분 수열이 비어있다면 첫 원소 삽입
if(index == 0) {
lis[index] = permut[i];
memo[i] = index;
index++;
}
else {
// 만약 현재 원소가 최장 증가 부분 수열의 원소라면 맨 마지막에 삽입
if(lis[index - 1] < permut[i]) {
lis[index] = permut[i];
memo[i] = index;
index++;
}
// 아닌 경우, lower bound로 삽입될 위치 탐색
else {
int l = 0;
int r = index - 1;
int mid;
// 대소 관계에 따라 두 부분으로 나누며 검색
while(l < r) {
mid = (l + r) / 2;
if(lis[mid] < permut[i])
l = mid + 1;
// lower bound는 그 수보다 작지 않은 최초의 인덱스를 찾으므로,
// r에는 mid 값에 1을 더하지 않음
else
r = mid;
}
// lower bound 위치에 현재 원소 삽입 및 부분 수열에서의 위치 저장
lis[r] = permut[i];
memo[i] = r;
}
}
}
// 찾은 최장 증가 부분 수열의 길이 출력
cout << index << '\n';
// 최장 증가 부분 수열의 원소 탐색
vector<long> order;
for(int i = n - 1; i >= 0; i--) {
// 수열의 길이를 줄여나가며, 각 길이에 대한 최장 증가 부분 수열 탐색
if(memo[i] == index - 1) {
order.push_back(permut[i]);
index--;
}
}
// 찾은 부분 수열을 역순으로 출력
while(!order.empty()) {
cout << order.back() << ' ';
order.pop_back();
}
cout << endl;
return 0;
}