A → B
백준 16953
SILVER II
문제 내용
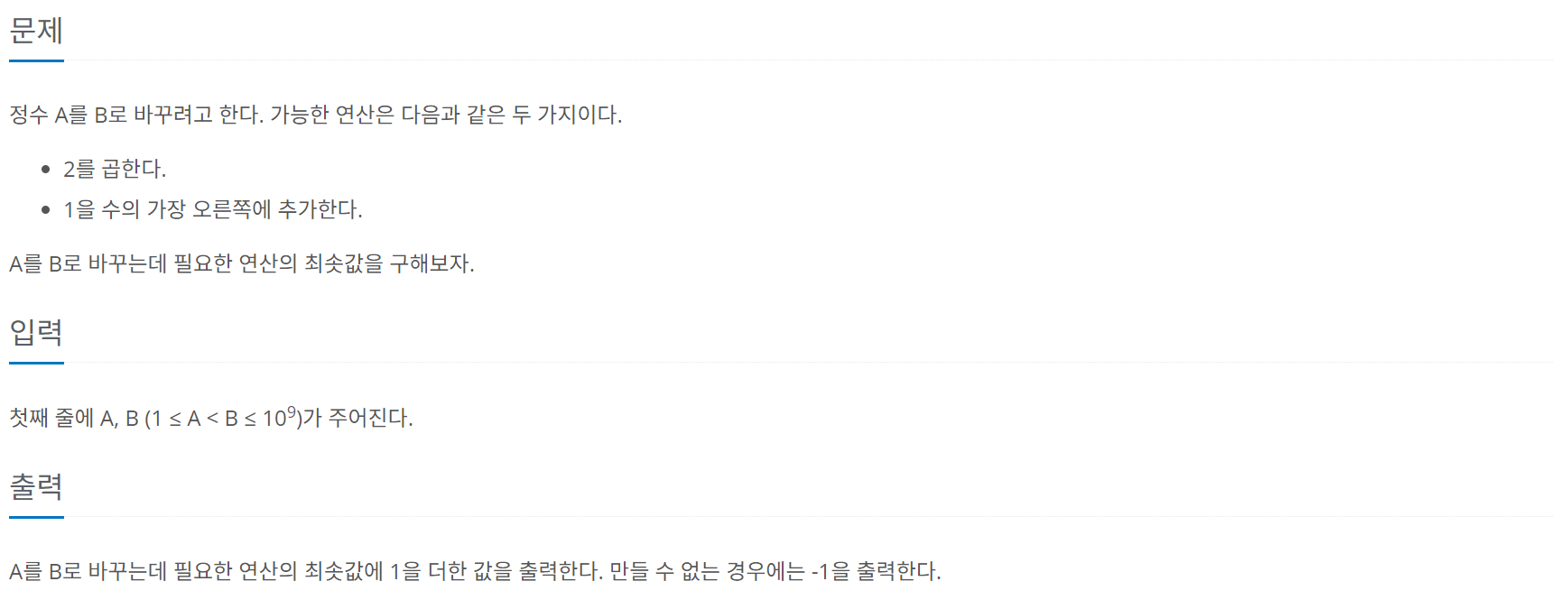
문제 링크
해결 방안
임의의 숫자에 2를 곱하거나 값의 오른쪽에 1을 추가하는 과정을 반복할 때, 원하는 숫자를 만들 수 있는지 판별하는 문제이다. 해결 여부를 판별하기 위한 별다른 공식이 없기 때문에, 모든 결과를 탐색해야 한다. 다양한 방법으로 해결할 수 있겠지만, 직관적인 풀이를 위해 너비 우선 탐색(BFS) 알고리즘을 사용하기로 한다.
먼저, 모든 결과에 대해 너비 우선 탐색으로 값을 저장하기 위한 자료구조인 큐를 생성해야 한다. 그리고 맨 처음 숫자에 대해 2를 곱하는 연산과 값의 오른쪽에 1을 추가하는 연산을 각각 실행한 결과를 큐에 넣는다. 각각의 연산 결과에 대해 다시 2를 곱하거나 1을 추가한 연산을 실행하고, 다시 그 결과들을 큐에 넣는다. 두 연산 결과가 기존의 값보다 커지기 때문에, 원하는 숫자보다 큰 값에 아무리 연산을 하더라도 원하는 숫자를 만들 수 없다. 때문에, 만약 연산 결과가 원하는 값보다 커지면 연산을 중단하고, 모든 연산 결과가 원하는 값보다 커져 더이상 연산할 수 없다면 원하는 숫자를 만들 수 없는 것으로 간주한다.
본 문제에서 요구하는 답은 해당 결과까지 필요한 연산의 수이므로, 각 연산의 결과에 지금까지의 연산 횟수를 같이 저장한다. 여기서 해결한 방식 외에도 두 개의 큐를 만들어, 첫 번째 큐에서 꺼낸 값들에 2를 곱하거나 값의 오른쪽에 1을 추가하는 연산을 한 결과를 모두 두 번째 큐에 저장하는 방법도 있다. 이 경우에는 첫 번째 큐의 값이 모두 사라지면 두 번째 큐의 값을 모두 첫 번째 큐로 옮기고, 옮기는 과정을 한 횟수가 필요한 연산 횟수가 된다. 이 역시 연산 결과가 원하는 숫자보다 작을 때만 취급하고, 양쪽 큐에 모두 값이 없으면 불가능한 것으로 간주하면 된다.
너비 우선 탐색(Breadth First Search; BFS)이란?
그래프에서 임의의 노드를 기준으로 인접한 노드부터 탐색하는 알고리즘이다. 트리나 그래프의 임의의 노드와의 깊이(depth)가 가장 작은 노드(인접 노드)를 가장 처음에 방문하고, 깊이가 가장 큰 노드를 가장 마지막에 방문하게 된다. 시작 노드와 인접한 노드들부터 시작하여 인접한 노드들과 인접한 아직 탐색하지 않은 노드들로 뻗어나가기 때문에, FIFO(First In First Out) 방식의 자료구조인 큐(queue)를 사용해야 한다.
풀이 코드
#include <iostream>
#include <queue>
using namespace std;
int main() {
// 시작하는 수 a와 만들고자 하는 수 b
long long a, b;
cin >> a >> b;
// bfs를 위한 큐(first: 연산 결과, second: 연산 횟수)
queue<pair<long long, long>> q;
pair<long long, long> top;
// a 값에서부터 시작
q.push({a, 1});
while(!q.empty()) {
top = q.front();
q.pop();
// 현재 연산 결과가 원하는 숫자와 같다면 출력 후 종료
if(top.first == b) {
cout << top.second << endl;
return 0;
}
// 각 연산의 결과가 원하는 숫자 초과면 연산 결과를 취급하지 않음
// 그 외에는 연산 결과와 현재 연산 횟수에 1을 더하여 저장
if(top.first * 2 <= b)
q.push({top.first * 2, top.second + 1});
if(top.first * 10 + 1 <= b)
q.push({top.first * 10 + 1, top.second + 1});
}
// 만약 큐에 값이 없을 때까지 원하는 숫자가 안 나오면 불가능 한 것으로 간주
cout << -1 << endl;
return 0;
}