이분 탐색(Binary Search)
이분 탐색이란?
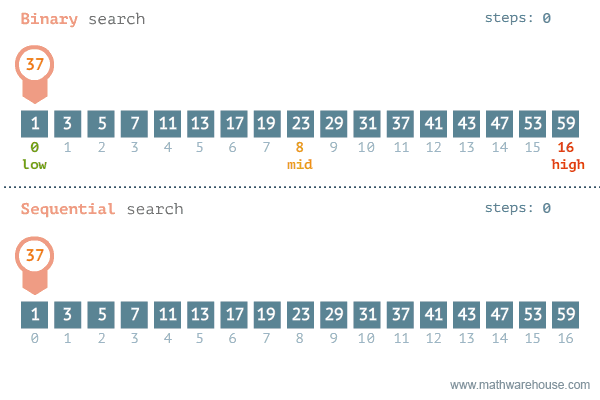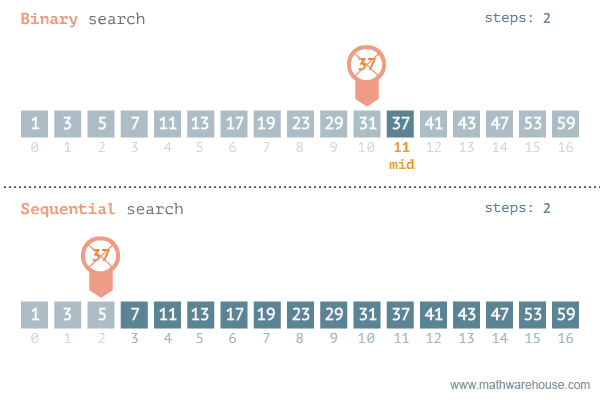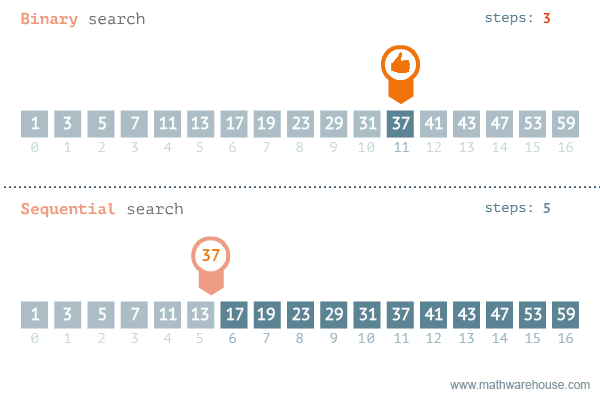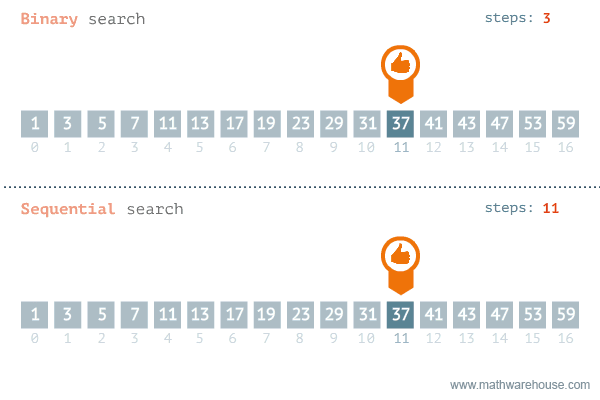
이분 탐색 혹은 이진 탐색이라고 불리는 이 알고리즘은 임의의 리스트를 두 부분으로 나누어가며 원하는 값이 나올 때까지 반복하여 탐색하는 방법이다. 원하는 값을 탐색하는 동안 검색 범위를 계속해서 두 부분으로 나누기 때문에, 이분 혹은 이진이라는 이름이 붙었다.
source: https://www.mathwarehouse.com
탐색 과정
이분 탐색을 사용하기 위해서는 반드시 리스트 또는 배열이 정렬되어 있어야 한다. 이는 이분 탐색을 위해 검색 범위를 두 부분으로 나누었을 때, 원하는 값이 두 부분 중 어느 부분에 있는 지 찾기 위함이다. 오름차순으로 정렬된 리스트에서 이분 탐색으로 임의의 값을 탐색하는 과정은 다음과 같다.
- 임의의 리스트의 처음과 마지막의 인덱스의 평균, 즉 처음 인덱스와 마지막 인덱스를 합한 값을 2로 나눈 인덱스를 중간 인덱스로 정한다.
- 중간 인덱스의 값을 확인하고, 찾고 있는 값이 해당 인덱스의 값보다 큰 지 작은 지 판별한다.
- 리스트가 오름차순으로 정렬되어 있기 때문에, 찾고 있는 값이 더 크다면 중간 인덱스보다 더 큰 인덱스에, 더 작다면 중간 인덱스보다 더 작은 인덱스에 위치해 있다.
- 찾고 있는 값이 더 크다면, 중간 인덱스를 처음 인덱스로 바꾸어 다시 처음과 마지막 인덱스의 평균을 중간 인덱스로 정하여 지금까지의 과정을 반복한다.
- 반대로 찾고 있는 값이 더 작다면, 중간 인덱스를 마지막 인덱스로 바꾸어 다시 처음과 마지막 인덱스의 평균을 중간 인덱스로 정하여 지금까지의 과정을 반복한다.
- 중간 인덱스가 찾고 있는 값인 경우, 현재까지의 과정을 중단한다.
- 처음 인덱스와 마지막 인덱스가 같음에도 중간 인덱스가 찾고 있는 값이 아닌 경우, 현재 리스트에는 찾고 있는 값이 없는 것이다.
예제 코드
위의 탐색 과정을 바탕으로 C++로 임시 구현한 코드는 다음과 같다.
int n; // 배열의 크기
int array[n]; // 크기가 n인 배열
// target을 발견하면, 해당 인덱스를 반환
// 만약 배열 안에 target이 없다면, -1 반환
int BinarySearch(int target) {
int start = 0; // 처음 인덱스(초깃값: 배열의 첫번째 인덱스)
int end = n - 1; // 마지막 인덱스(초깃값: 배열의 마지막 인덱스)
// 처음 인덱스와 마지막 인덱스가 하나의 인덱스를 지정할 때까지 반복
while(start <= end) {
// 처음 인덱스와 마지막 인덱스의 중간 인덱스
int mid = (start + end) / 2;
// 중간 인덱스가 찾고 있는 값인 경우, 인덱스 반환 및 탐색 종료
if(array[mid] == target)
return mid;
// 찾고 있는 값이 중간 인덱스보다 크다면, 값이 더 큰 부분에서 탐색
if(array[mid] < target)
start = mid + 1;
// 찾고 있는 값이 중간 인덱스보다 작다면, 값이 더 작은 부분에서 탐색
else if(array[mid] > target)
end = mid - 1;
// 현재의 중간 인덱스는 target 값이 아니므로, 인덱스 범위에서 제외
// 처음 인덱스와 마지막 인덱스가 같을 때에도 찾고 있는 값이 아니라면,
// 마지막 인덱스가 처음 인덱스 앞의 인덱스에 위치하게 되어 탐색 종료
}
// 인덱스를 찾지 못하면 -1 반환
return -1;
}
이진 탐색은 처음 인덱스와 마지막 인덱스의 중간 인덱스를 기준으로, 탐색 대상과의 대소 관계를 비교하여 나누어진 두 부분에 대해 같은 방식으로 탐색을 진행한다. 이를 위해서는 반드시 리스트가 정렬되어 있어야 한다.
하한값 탐색(Lower Bound)
이분 탐색은 찾고자 하는 값이 없다면, 찾는 값이 없음을 나타내고 탐색을 종료한다. 하지만, 문제에 따라서는 찾는 값이 반드시 찾아야 하는 값이 아닌 최소 조건이 될 수도 있다. 이번에 설명할 알고리즘은 이분 탐색의 종류 중 하나인 하한값 탐색(lower bound)이다.
lower bound는 찾고자 하는 값 이상이 되는 값이 처음으로 나타나는 인덱스를 반환한다. 아래의 lower bound 예제 코드에서 이분 탐색과의 차이를 대조해보자.
예제 코드
int n;
int array[n];
int LowerBound(int target) {
int start = 0;
int end = n - 1;
// 두 인덱스가 하나의 인덱스를 가리킬 때까지 반복
while(start < end) {
int mid = (start + end) / 2;
if(array[mid] < target)
start = mid + 1;
// 중간 인덱스의 값이 찾는 값 이상이면, 마지막 인덱스를 중간 인덱스로 설정
else
end = mid;
}
// 마지막 인덱스 반환
return end;
}
이분 탐색에서는 찾고자 하는 값이 중간 인덱스의 값보다 작다면, 중간 인덱스를 제외한 더 작은 값이 있는 범위에서 탐색을 진행했다. 하지만, lower bound는 그 중간 인덱스를 포함하여 탐색을 진행한다.
만약 중간 인덱스가 찾는 값보다 작다면, 처음 인덱스가 마지막 인덱스 방향으로 움직이게 된다. 반대로 중간 인덱스가 찾는 값보다 크다면, 마지막 인덱스를 그 중간 인덱스로 움직인다. 결과적으로, 값을 찾지 못하더라도 마지막 인덱스가 찾는 값의 이상인 인덱스에서 고정되기 때문에, 두 인덱스가 만나는 지점이 찾고자 하는 값 이상이 되는 첫 인덱스이다. 당연하게도 찾고자 하는 값 이상인 값이기 때문에 찾고자 하는 값과 똑같은 값이 있다면, 이분 탐색처럼 그대로 반환된다.
하한값 탐색은 찾고자 하는 값 이상이 되는 값이 처음으로 나타나는 인덱스를 찾는 이진 탐색 알고리즘이다.
상한값 탐색(Upper Bound)
하한값 탐색(lower bound)이 찾고자 하는 값 이상이 되는 값이 처음으로 나타나는 인덱스를 반환한다면, 상한값 탐색(upper bound)은 찾고자 하는 값보다 큰 값이 처음으로 나타나는 인덱스를 반환한다. 어떻게 차이가 나는지는 아래의 예제 코드를 통해 알아보자.
예제 코드
int n;
int array[n];
int UpperBound(int target) {
int start = 0;
int end = n - 1;
while(start < end) {
int mid = (start + end) / 2;
// lower bound와 upper bound의 차이점이 드러나는 부분
// upper bound는 찾는 값을 발견해도 더 큰 부분을 탐색
if(array[mid] <= target)
start = mid + 1;
else
end = mid;
}
return end;
}
위 코드처럼 upper bound는 탐색 대상보다 더 큰 값이 있는 첫 인덱스를 반환하므로, 찾는 값과 중간 인덱스의 값이 같더라도 더 큰 부분에서 탐색을 계속한다. 중간 인덱스가 처음 인덱스와 마지막 인덱스의 평균에서 소숫점을 버리기 때문에, 중간 인덱스 값이 찾는 값보다 크면 마지막 인덱스가 처음 인덱스 방향으로 이동하게 된다. 결과적으로, 더 큰 값만이 있는 부분에서는 처음 인덱스가 고정된 채로 마지막 인덱스와 만나게 되어, 탐색 대상보다 더 큰 값이 있는 첫 인덱스를 반환하게 된다.
상한값 탐색은 찾고자 하는 값보다 큰 값이 처음으로 나타나는 인덱스를 찾는 이진 탐색 알고리즘이다.
정리
이분 탐색의 시간 복잡도는 리스트를 절반씩 나누어 탐색하기 때문에 O(log₂N)으로, 모든 수를 일일이 확인하는 선형 탐색(Linear Search)이 시간 복잡도가 O(N)인걸 고려하면 매우 빠르다는 것을 알 수 있다. 대신 이분 탐색을 사용하기 위해서는 리스트가 정렬되어 있어야만 한다. 이는 하한값 탐색과 상한값 탐색도 마찬가지인 사항으로, 정렬되기만 한다면 이 역시 O(log₂N)만에 원하는 값을 얻을 수 있다.
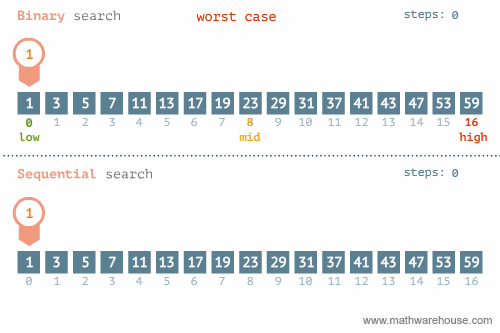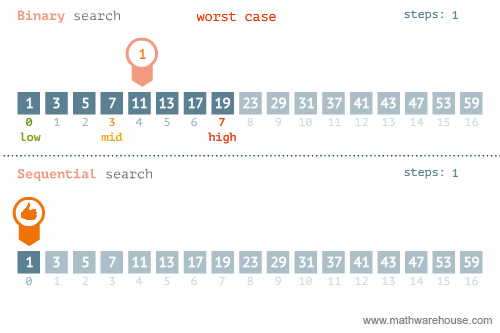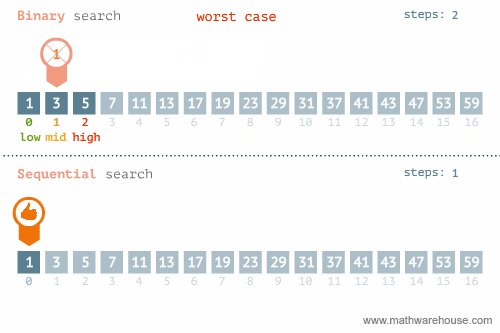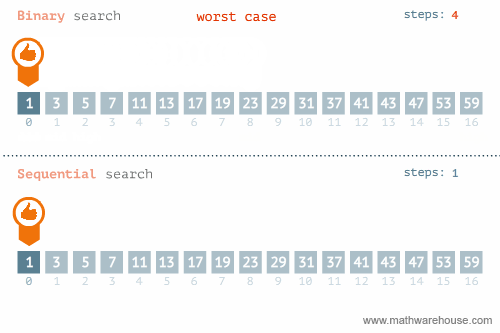
source: https://www.mathwarehouse.com
이진 탐색의 시간 복잡도는 O(log₂N)이고, 이를 위해서는 반드시 리스트나 배열이 정렬되어 있어야 한다.
관련 문제 추천
- 이분 탐색 : 백준 1920번: 수 찾기
- 하한값 탐색 : 백준 12015번: 가장 긴 증가하는 부분 수열 2
- 상한값 탐색 : 백준 2143번: 두 배열의 합